Sinyal dan Sistem Linear
Kata lain sinyal adalah isyarat. Tapi penggunaan sehari-hari kata "sinyal" dan kata "isyarat" sedikit berbeda. Seseorang menyuruh diam dengan meletakkan telunjuk ke bibir disebut memberi isyarat. Kereta berangkat menunggu sinyal dari petugas PPKA berupa tiupan peluit.
Dalam pembicaraan tentang sistem teknik, kedua kata di atas adalah sama. Sinyal adalah besaran yang diamati dalam selang waktu tertentu. Dalam selang waktu yang dimaksud, biasanya besaran berubah secara dinamis. Dalam keseharian dikenal sinyal suara atau sinyal gambar yang besarannya senantiasa berubah
terhadap waktu. Namun besaran yang tidak berubah terhadap waktu secara teknis disebut sinyal juga asalkan merupakan pengamatan dalam selang waktu tertentu. Sehingga cahaya yang keluar dari sebuah lampu (meskipun intensitasnya tetap) disebut sinyal cahaya. Sebuah sepeda motor mempunyai besaran fisik: berat, warna, ukuran, kecepatan, jumlah persnelling, dan lain-lain. Semuanya adalah sinyal yang dikeluarkan oleh sepeda motor jika diamati dalam selang waktu tertentu. Namun di antara besaran-besaran yang dimiliki oleh sepeda motor, mungkin hanya kecepatan yang sifatnya dinamis, besaran lain bersifat statis. Oleh karena itu kecepatan merupakan besaran yang paling banyak diamati/diperhatikan untuk sepeda motor.
Pembicaraan tentang sistem seringkali melibatkan pembicaraan tentang sinyal. Sistem dikenali dari sinyal yang dikeluarkannya, dan sistem diamati karena ada dinamika sinyal padanya. Masukan dan keluaran sistem berwujud sinyal. Masukan dari sistem audio adalah sinyal magnetis dari pita kaset dan keluarannya adalah sinyal suara. Dalam sistem bendungan, aliran air ke persawahan adalah sinyal, aliran air dari hulu adalah sinyal, hujan adalah sinyal, pengubahan posisi pintu air oleh petugas irigasi adalah sinyal, bahkan watt listrik yang dihasilkan (jika ada PLTA-nya) adalah sinyal.
Secara teknis sinyal dibedakan menurut keberadaan dan nilai besarannya. Gambar berikut ini memperlihatkan empat macam sinyal yaitu: sinyal kontinyu (analog), sinyal kontinyu terkuantisasi, sinyal diskret, dan sinyal diskret terkuantisasi (digital).

Sinyal kontinyu merupakan bentuk kebanyakan sinyal yang ada di alam. Debit aliran air sungai, arus listrik yang masuk ke sebuah rumah pelanggan PLN dan suhu suatu ruangan adalah contohnya. Sinyal kontinyu mempunyai nilai di semua waktu dan nilainya bisa berapa saja. Sinyal kontinyu terkuantisasi mempunyai nilai di semua waktu tapi nilainya hanya tertentu saja. Contohnya adalah nilai tukar rupiah terhadap dollar, atau harga suatu barang di toko. Sinyal diskret mempunyai nilai pada waktu-waktu tertentu saja dan nilainya bisa berapa saja. Contohnya adalah data harian curah hujan di Solo, atau nilai indeks harga saham gabungan di bursa pada saat penutupan transaksi. Sinyal diskret terkuantisasi mempunyai nilai pada waktu-waktu tertentu saja dan nilainya hanya tertentu. Contohnya adalah sinyal komunikasi digital. Pembicaraan dalam kuliah sistem linier secara umum adalah menyangkut sinyal kontinyu dan diskret yang tidak terkuantisasi.
Sistem Linier
Sistem linier adalah sistem dengan sifat khusus berupa linieritas. Artinya hubungan masukan dan keluarannya bersifat linier. Jika digambar pada grafik hubungan itu berupa garis lurus. Namun gambaran grafis berupa garis lurus hanya berlaku pada saat sistem berada pada kondisi mantap (steady) dan bukan pada kondisi transisi (transien). Jika resistor tiba-tiba diberi tegangan, arus resistor tidak langsung muncul sesuai hukum ohm. Ada masa transisi dari kondisi belum diberi tegangan (kondisi awal) menuju kondisi mantap (meskipun hanya dalam hitungan mikrodetik atau nanodetik). Hukum ohm hanya berlaku pada kondisi mantap. Kondisi transisi ini tidak diperhatikan pada desain rangkaian elektronik biasa, tapi kondisi ini menjadi perhatian pada sistem frekuensi tinggi di mana sinyal berubah dengan sangat cepat.
Ada dua alasan penting mengapa studi sistem linier menjadi perlu:
Sistem Linier Time Invariant
2 Hal penting pada system adalah linieritas dan tidak berubah terhadap waktu.
Disini akan dilihat hubungan input-output pada system LTI dijelaskan pada operasi konvolusi.
Respons system LTI waktu kontinyu dan Integral Konvolusi
Respon Sistem Linier Time Invariant (LTI) dalam waktu kontinyu dan diskrit dapat dicari dengan metode konvolusi jika respon impulsnya diketahui.Pada siitem waktu kontinyu respon sistem ditentukan dengan menghitung integral konvolusi. Pada sistem diskrit respon sistem ditentukan dengan konvolusi sinyal diskrit.
Representasi deret fourier sinyal periodik
Deret fourier adalah deret yang digunakan dalam bidang rekayasa. Deret ini pertama kali ditemukan oleh seorang ilmuan perancis Jean-Baptiste Joseph Fourier (1768-1830). Derat yang selanjutnya dikenal sebagai deret fourier ini merupakan deret dalam bentuk sinusoidal (sinus dan cosinus) yang digunakan untuk merepresentasikan fungsi-fungsi periodik secara umum. Selain itu, deret ini juga sering dijadikan sebagai alat bantu dalam menyelasaikan persamaan diferensial, baik persamaan diferensial biasa maupun persamaan diferensial parsial. Teori dasar deret fourier cukup rumit. Meskipun demikian, aplikasinya cukup sederhana.
Deret fourier dapat dituliskan dengan persamaan sebagai berikut: f(t) = A0 + A1 cos ?t + B1 sin ?t + … An cos n?t + Bn sin n?t.
Salah satu aplikasi dari deret fourier adalah pada pemisahan perpaduan gelombang. Suatu gelombang yang bergerak pada sutu medium bukan hanya gelombang yang berupa gelombang tunggal namun merupakan perpaduan dari banyak gelombang. Dengan menggunakan deret fourier maka perpaduan dari banyak panjang gelombang ini dapat dipisahkan kembali menjadi gelombang-gelombang penyusunnya. Misalkan saja pada gelombang radio. Gelombang radio FM mempunyai frekuensi 88 Mhz sampai dengan 108 Mhz. Tapi yang menimbulkan pertanyaan adalah kenapa kita dapat mendengarkan suara penyiar radionya padahal batas pendengaran manusia hanya 20 Hz sampai dengan 20.000 Hz saja?. Ini dapat dijawab karena gelombang radio tersebut hanya sebagai pembawa. Yang nantinya pada radio penerima gelombang datang tersebut akan dipecah kembali yang salah satunya berupa gelombang suara yang dapat kita dengarkan.
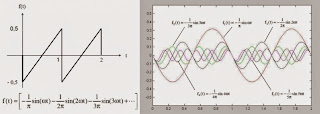
Pada gambar diatas disajikan dua bentuk gelombang yang mempunyai bentuk yang sangat berbeda. Namun pada gambar kiri itu merupakan gelombang perpaduan dari banyak sekali gelombang. Sedangkan pada gambar kanan merupakan bentuk-bentuk gelombang yang menyusun gambar kiri tadi. Gambar kiri dapat di pecah menjadi gambar kanan dengan bantuan deret fourier. Hal ini pula yang berlaku pada frekuensi radio yang telah disinggung sebelumnya. Selain adanya deret fourier, juga dikenal adanya transformasi fourier (Fourier Transform-FT). Joseph Fourier mengemukakan bahwa sebuah fungsi periodik dapat direpresentasikan dengan mengkombinasikan penjumlahan tak hingga dari fungsi sinus dan cosinus. Representasi fungsi inilah yang kemudian dikenal sebagai Deret Fourier. Beberapa tahun setelah penemuan ini, deret fourier dikembangkan menjadi bentuk yang lebih umum sehingga dapat diterapkan pada fungsi yang non-periodik, bentuk yang lebih umum ini yang kemudian dikenal sebagai Transformasi Fourier (FT). Sejak penemuan ini, transformasi fourier menjadi metoda yang sangat cocok untuk menganalisis fungsi atau sinyal1, karena transformasi fourier dapat mengubah fungsi atau sinyal dalam domain waktu ke domain frekuensi.
Biasanya sebuah fungsi digambarkan dalam domain waktu. Artinya yang diukur dari fungsi tersebut adalah waktu. Dengan kata lain, jika kita gambarkan fungsi tersebut pada sumbu simetri, maka sumbu x (sebagai variabel bebas) mewakili waktu, dan sumbu y (sebagai variabel tak bebas) mewakili nilai pada waktu t tertentu, atau nilai amplitudo-nya.
Jika kita menggambar fungsi dalam domain waktu, maka kita akan memperoleh representasi waktu-amplitudo fungsi tersebut. Pada aplikasinya, representasi ini tidak selalu merupakan representasi terbaik. Pada banyak kasus, informasi khusus tersembunyi pada nilai frekuensinya. Spektrum frekuensi dari sebuah fungsi memperlihatkan frekuensi yang termuat pada fungsi tersebut.
Transformasi Fourier (Fourier Transform atau FT) dapat mengubah fungsi atau sinyal dalam domain waktu ke dalam domain frekuensi. Jika kita menerapkan FT pada sebuah fungsi dalam domain waktu, maka kita akan mendapatkan repesentasi frekuensi-amplitudo fungsi tersebut. Dengan transformasi fourier, sebuah fungsi dapat digambarkan dalam sumbu x yang menunjukkan spektrum frekuensi dan sumbu y menunjukkan amplitudo. Gambar FT menunjukkan berapa banyak frekuensi yang termuat pada fungsi tersebut.
Berikut ini adalah contoh dua buah fungsi stasioner periodik, yang tergabungkan (y1 + y2 = y) beserta gambar FT-nya:
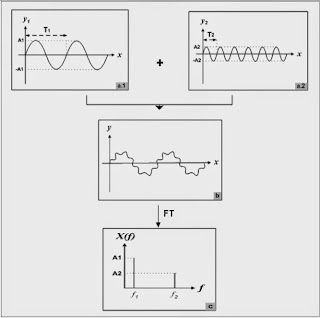
Seringkali, informasi yang tidak dapat dilihat pada domain waktu, dapat dilihat pada domain frekuensi. Sebagai contoh dalam bidang medis dikenal sinyal ECG (ElectroCardioGraphy), yaitu catatan grafik aktivitas elektrik jantung. Bentuk khusus ECG orang yang sehat, dikenal betul oleh seorang ahli jantung. Sebuah penyimpangan yang berarti dari bentuk tersebut biasanya dianggap sebagai gejala adanya penyakit. Namun gejala adanya penyakit tidak selalu terlihat jelas pada sinyal ECG dalam domain waktu, terkadang penyakit dapat didiagnosa lebih mudah jika sinyal dianalisis dalam domain frekuensi. Pada ECG dapat memanfaatkan transformasi fourier tergantung yang diinginkan. Seperti telah disinggung sebelumnya bahwa tidak selalu suatu gejala kejanggalan pembacaan catatan grafik aktifitas elektrik jantung dapat teramati dengan baik dalam domain waktu. Sehingga diperlukan domain lain yang sesuai dan dapat memberikan informasi yang lebih akurat kepada pembaca. Domain lain yang dapat digunakan adalah domain frekuensi. Dan sebaliknya tidak semua gejala kejanggalan juga dapat dibaca pada domain ini. Sehingga antara doain waktu dan domain frekuensi akan saling melengkapi, tergantung dengan kebutuhan. Hal tersebut merupakan contoh sederhana dari kegunaan domain frekuensi. Transformasi fourier bersifat reversibel, yaitu suatu fungsi dapat ditransformasi ke dalam domain frekuensi (yang memuat informasi frekuensi amplitudo), dan di inversikan lagi ke domain waktu (yang memuat informasi waktu-amplitudo). Namun, kedua informasi tersebut tidak bisa didapatkan secara bersamaan. Representasi fungsi dalam domain frekuensi tidak memuat informasi waktu, demikian pula sebaliknya. Untuk fungsi-fungsi yang stasioner, yaitu fungsi yang nilai frekuensinya tidak berubah-ubah secara kontinu, informasi waktu dan frekuensi secara bersamaan tidak diperlukan, karena di seluruh interval waktu, nilai komponen frekuensinya konstan.
Kata lain sinyal adalah isyarat. Tapi penggunaan sehari-hari kata "sinyal" dan kata "isyarat" sedikit berbeda. Seseorang menyuruh diam dengan meletakkan telunjuk ke bibir disebut memberi isyarat. Kereta berangkat menunggu sinyal dari petugas PPKA berupa tiupan peluit.
Dalam pembicaraan tentang sistem teknik, kedua kata di atas adalah sama. Sinyal adalah besaran yang diamati dalam selang waktu tertentu. Dalam selang waktu yang dimaksud, biasanya besaran berubah secara dinamis. Dalam keseharian dikenal sinyal suara atau sinyal gambar yang besarannya senantiasa berubah
terhadap waktu. Namun besaran yang tidak berubah terhadap waktu secara teknis disebut sinyal juga asalkan merupakan pengamatan dalam selang waktu tertentu. Sehingga cahaya yang keluar dari sebuah lampu (meskipun intensitasnya tetap) disebut sinyal cahaya. Sebuah sepeda motor mempunyai besaran fisik: berat, warna, ukuran, kecepatan, jumlah persnelling, dan lain-lain. Semuanya adalah sinyal yang dikeluarkan oleh sepeda motor jika diamati dalam selang waktu tertentu. Namun di antara besaran-besaran yang dimiliki oleh sepeda motor, mungkin hanya kecepatan yang sifatnya dinamis, besaran lain bersifat statis. Oleh karena itu kecepatan merupakan besaran yang paling banyak diamati/diperhatikan untuk sepeda motor.
Pembicaraan tentang sistem seringkali melibatkan pembicaraan tentang sinyal. Sistem dikenali dari sinyal yang dikeluarkannya, dan sistem diamati karena ada dinamika sinyal padanya. Masukan dan keluaran sistem berwujud sinyal. Masukan dari sistem audio adalah sinyal magnetis dari pita kaset dan keluarannya adalah sinyal suara. Dalam sistem bendungan, aliran air ke persawahan adalah sinyal, aliran air dari hulu adalah sinyal, hujan adalah sinyal, pengubahan posisi pintu air oleh petugas irigasi adalah sinyal, bahkan watt listrik yang dihasilkan (jika ada PLTA-nya) adalah sinyal.
Secara teknis sinyal dibedakan menurut keberadaan dan nilai besarannya. Gambar berikut ini memperlihatkan empat macam sinyal yaitu: sinyal kontinyu (analog), sinyal kontinyu terkuantisasi, sinyal diskret, dan sinyal diskret terkuantisasi (digital).
Sinyal kontinyu merupakan bentuk kebanyakan sinyal yang ada di alam. Debit aliran air sungai, arus listrik yang masuk ke sebuah rumah pelanggan PLN dan suhu suatu ruangan adalah contohnya. Sinyal kontinyu mempunyai nilai di semua waktu dan nilainya bisa berapa saja. Sinyal kontinyu terkuantisasi mempunyai nilai di semua waktu tapi nilainya hanya tertentu saja. Contohnya adalah nilai tukar rupiah terhadap dollar, atau harga suatu barang di toko. Sinyal diskret mempunyai nilai pada waktu-waktu tertentu saja dan nilainya bisa berapa saja. Contohnya adalah data harian curah hujan di Solo, atau nilai indeks harga saham gabungan di bursa pada saat penutupan transaksi. Sinyal diskret terkuantisasi mempunyai nilai pada waktu-waktu tertentu saja dan nilainya hanya tertentu. Contohnya adalah sinyal komunikasi digital. Pembicaraan dalam kuliah sistem linier secara umum adalah menyangkut sinyal kontinyu dan diskret yang tidak terkuantisasi.
Sistem Linier
Sistem linier adalah sistem dengan sifat khusus berupa linieritas. Artinya hubungan masukan dan keluarannya bersifat linier. Jika digambar pada grafik hubungan itu berupa garis lurus. Namun gambaran grafis berupa garis lurus hanya berlaku pada saat sistem berada pada kondisi mantap (steady) dan bukan pada kondisi transisi (transien). Jika resistor tiba-tiba diberi tegangan, arus resistor tidak langsung muncul sesuai hukum ohm. Ada masa transisi dari kondisi belum diberi tegangan (kondisi awal) menuju kondisi mantap (meskipun hanya dalam hitungan mikrodetik atau nanodetik). Hukum ohm hanya berlaku pada kondisi mantap. Kondisi transisi ini tidak diperhatikan pada desain rangkaian elektronik biasa, tapi kondisi ini menjadi perhatian pada sistem frekuensi tinggi di mana sinyal berubah dengan sangat cepat.
Ada dua alasan penting mengapa studi sistem linier menjadi perlu:
- Model sistem linier dapat dipelajari lebih mudah dan pembahasannya telah mendalam. Alat bantu analisis dan desain sistem linier telah banyak tersedia.
- Kebanyakan sistem fisik dapat dimodelkan dengan sistem linier.
Sistem Linier Time Invariant
2 Hal penting pada system adalah linieritas dan tidak berubah terhadap waktu.
Disini akan dilihat hubungan input-output pada system LTI dijelaskan pada operasi konvolusi.
Respons system LTI waktu kontinyu dan Integral Konvolusi
Respon Sistem Linier Time Invariant (LTI) dalam waktu kontinyu dan diskrit dapat dicari dengan metode konvolusi jika respon impulsnya diketahui.Pada siitem waktu kontinyu respon sistem ditentukan dengan menghitung integral konvolusi. Pada sistem diskrit respon sistem ditentukan dengan konvolusi sinyal diskrit.
Representasi deret fourier sinyal periodik
Deret fourier adalah deret yang digunakan dalam bidang rekayasa. Deret ini pertama kali ditemukan oleh seorang ilmuan perancis Jean-Baptiste Joseph Fourier (1768-1830). Derat yang selanjutnya dikenal sebagai deret fourier ini merupakan deret dalam bentuk sinusoidal (sinus dan cosinus) yang digunakan untuk merepresentasikan fungsi-fungsi periodik secara umum. Selain itu, deret ini juga sering dijadikan sebagai alat bantu dalam menyelasaikan persamaan diferensial, baik persamaan diferensial biasa maupun persamaan diferensial parsial. Teori dasar deret fourier cukup rumit. Meskipun demikian, aplikasinya cukup sederhana.
Deret fourier dapat dituliskan dengan persamaan sebagai berikut: f(t) = A0 + A1 cos ?t + B1 sin ?t + … An cos n?t + Bn sin n?t.
Salah satu aplikasi dari deret fourier adalah pada pemisahan perpaduan gelombang. Suatu gelombang yang bergerak pada sutu medium bukan hanya gelombang yang berupa gelombang tunggal namun merupakan perpaduan dari banyak gelombang. Dengan menggunakan deret fourier maka perpaduan dari banyak panjang gelombang ini dapat dipisahkan kembali menjadi gelombang-gelombang penyusunnya. Misalkan saja pada gelombang radio. Gelombang radio FM mempunyai frekuensi 88 Mhz sampai dengan 108 Mhz. Tapi yang menimbulkan pertanyaan adalah kenapa kita dapat mendengarkan suara penyiar radionya padahal batas pendengaran manusia hanya 20 Hz sampai dengan 20.000 Hz saja?. Ini dapat dijawab karena gelombang radio tersebut hanya sebagai pembawa. Yang nantinya pada radio penerima gelombang datang tersebut akan dipecah kembali yang salah satunya berupa gelombang suara yang dapat kita dengarkan.

Pada gambar diatas disajikan dua bentuk gelombang yang mempunyai bentuk yang sangat berbeda. Namun pada gambar kiri itu merupakan gelombang perpaduan dari banyak sekali gelombang. Sedangkan pada gambar kanan merupakan bentuk-bentuk gelombang yang menyusun gambar kiri tadi. Gambar kiri dapat di pecah menjadi gambar kanan dengan bantuan deret fourier. Hal ini pula yang berlaku pada frekuensi radio yang telah disinggung sebelumnya. Selain adanya deret fourier, juga dikenal adanya transformasi fourier (Fourier Transform-FT). Joseph Fourier mengemukakan bahwa sebuah fungsi periodik dapat direpresentasikan dengan mengkombinasikan penjumlahan tak hingga dari fungsi sinus dan cosinus. Representasi fungsi inilah yang kemudian dikenal sebagai Deret Fourier. Beberapa tahun setelah penemuan ini, deret fourier dikembangkan menjadi bentuk yang lebih umum sehingga dapat diterapkan pada fungsi yang non-periodik, bentuk yang lebih umum ini yang kemudian dikenal sebagai Transformasi Fourier (FT). Sejak penemuan ini, transformasi fourier menjadi metoda yang sangat cocok untuk menganalisis fungsi atau sinyal1, karena transformasi fourier dapat mengubah fungsi atau sinyal dalam domain waktu ke domain frekuensi.
Biasanya sebuah fungsi digambarkan dalam domain waktu. Artinya yang diukur dari fungsi tersebut adalah waktu. Dengan kata lain, jika kita gambarkan fungsi tersebut pada sumbu simetri, maka sumbu x (sebagai variabel bebas) mewakili waktu, dan sumbu y (sebagai variabel tak bebas) mewakili nilai pada waktu t tertentu, atau nilai amplitudo-nya.
Jika kita menggambar fungsi dalam domain waktu, maka kita akan memperoleh representasi waktu-amplitudo fungsi tersebut. Pada aplikasinya, representasi ini tidak selalu merupakan representasi terbaik. Pada banyak kasus, informasi khusus tersembunyi pada nilai frekuensinya. Spektrum frekuensi dari sebuah fungsi memperlihatkan frekuensi yang termuat pada fungsi tersebut.
Transformasi Fourier (Fourier Transform atau FT) dapat mengubah fungsi atau sinyal dalam domain waktu ke dalam domain frekuensi. Jika kita menerapkan FT pada sebuah fungsi dalam domain waktu, maka kita akan mendapatkan repesentasi frekuensi-amplitudo fungsi tersebut. Dengan transformasi fourier, sebuah fungsi dapat digambarkan dalam sumbu x yang menunjukkan spektrum frekuensi dan sumbu y menunjukkan amplitudo. Gambar FT menunjukkan berapa banyak frekuensi yang termuat pada fungsi tersebut.
Berikut ini adalah contoh dua buah fungsi stasioner periodik, yang tergabungkan (y1 + y2 = y) beserta gambar FT-nya:

Seringkali, informasi yang tidak dapat dilihat pada domain waktu, dapat dilihat pada domain frekuensi. Sebagai contoh dalam bidang medis dikenal sinyal ECG (ElectroCardioGraphy), yaitu catatan grafik aktivitas elektrik jantung. Bentuk khusus ECG orang yang sehat, dikenal betul oleh seorang ahli jantung. Sebuah penyimpangan yang berarti dari bentuk tersebut biasanya dianggap sebagai gejala adanya penyakit. Namun gejala adanya penyakit tidak selalu terlihat jelas pada sinyal ECG dalam domain waktu, terkadang penyakit dapat didiagnosa lebih mudah jika sinyal dianalisis dalam domain frekuensi. Pada ECG dapat memanfaatkan transformasi fourier tergantung yang diinginkan. Seperti telah disinggung sebelumnya bahwa tidak selalu suatu gejala kejanggalan pembacaan catatan grafik aktifitas elektrik jantung dapat teramati dengan baik dalam domain waktu. Sehingga diperlukan domain lain yang sesuai dan dapat memberikan informasi yang lebih akurat kepada pembaca. Domain lain yang dapat digunakan adalah domain frekuensi. Dan sebaliknya tidak semua gejala kejanggalan juga dapat dibaca pada domain ini. Sehingga antara doain waktu dan domain frekuensi akan saling melengkapi, tergantung dengan kebutuhan. Hal tersebut merupakan contoh sederhana dari kegunaan domain frekuensi. Transformasi fourier bersifat reversibel, yaitu suatu fungsi dapat ditransformasi ke dalam domain frekuensi (yang memuat informasi frekuensi amplitudo), dan di inversikan lagi ke domain waktu (yang memuat informasi waktu-amplitudo). Namun, kedua informasi tersebut tidak bisa didapatkan secara bersamaan. Representasi fungsi dalam domain frekuensi tidak memuat informasi waktu, demikian pula sebaliknya. Untuk fungsi-fungsi yang stasioner, yaitu fungsi yang nilai frekuensinya tidak berubah-ubah secara kontinu, informasi waktu dan frekuensi secara bersamaan tidak diperlukan, karena di seluruh interval waktu, nilai komponen frekuensinya konstan.






Komentar ini telah dihapus oleh pengarang.
BalasHapusTerimakasih, sangat membantu untuk memahami pengloahan sinyal secara simpel. Analogi dan contoh yang diberikan juga sesuai. Teruskan
BalasHapus